| Board | UP Board |
| Textbook | NCERT |
| Class | Class 12 |
| Subject | Physics |
| Model Paper | Paper 1 |
| Category | UP Board Model Papers |
UP Board Class 12 Physics Model Papers Paper 1
समय 3 घण्टे 15 मिनट
पूर्णांक 70
निर्देश
प्रारम्भ के 15 मिनट परीक्षार्थियों को प्रश्नपत्र पढ़ने के लिए निर्धारित हैं।
नोट
Table of Contents
Toggle- इस प्रश्न-पत्र में कुल पाँच प्रश्न हैं।
- सभी प्रश्न अनिवार्य हैं।
- प्रत्येक प्रश्न के जितने खण्ड हल करने हैं, उनकी संख्या प्रश्न के प्रारम्भ में लिखी है।
- प्रश्नों के अंक उनके सम्मुख लिखे हैं।
- प्रश्न-पत्र में प्रयुक्त प्रतीकों के सामान्य अर्थ हैं।
प्रश्न 1.
सभी खण्डों के उत्तर दीजिये।
(i) दो चालकीय गोले जिनकी त्रिज्यायें r1 तथा r2 ; हैं, समान आवेश घनत्व द्वारा आवेशित हैं। इनके पृष्ठों के निकट वैद्युत क्षेत्रों का अनुपात हैं।
(a) [latex]\cfrac { { r }_{ 1 }^{ 2 } }{ { r }_{ 2 }^{ 2 } } [/latex]
(b) [latex]\cfrac { { r }_{ 2 }^{ 2 } }{ { r }_{ 1 }^{ 2 } } [/latex]
(c) [latex]\cfrac { { r }_{ 1 }^{ } }{ { r }_{ 2 }^{ } } [/latex]
(d) 1:1
(ii) एक धात्विक प्रतिरोधक एक बैटरी से जुड़ा है। मुक्त इलेक्ट्रॉनों की प्रतिरोधक में धातु के धनायनों से टक्करों की संख्या कम होती हैं, तो धारा
(a) नियत रहेगी।
(b) बढ़ेगी।
(c) घटेगी
(d) शून्य हो जाएगी
(iii) डोमेन किस पदार्थ में बनते हैं?
(a) प्रतिचुम्बकीय ।
(b) लौहचुम्बकीय
(c) अनुचुम्बकीय
(d) इन सभी में
(iv) किसी कैथोड पृष्ठ का कार्यफलन 3.3 eV है। इस पृष्ठ से प्रकाश इलेक्ट्रॉनों के उत्सर्जन के लिए आपतित प्रकाश की न्यूनतम आवृत्ति होगी (h = 6.6 x 1034जूल-से)
(a) 6.6 x 10-34 हर्ट्ज
(b) 0.5 x 1034 हर्ट्ज
(c) 8 x 1014 हर्ट्ज
(d) 3.2 x 1015 हज़
(v) दूर दृष्टि दोष का निवारण होता है।
(a) उचित फोकस दूरी के अवतल लेन्स के प्रयोग से
(b) उचित फोकस दूरी के उत्तल लेन्स के प्रयोग से
(c) किसी भी अवतल लेन्स के प्रयोग से
(d) किसी भी उत्तल लेन्स के प्रयोग से
(vi) एक अर्द्ध-तरंगीय डायोड दिष्टकारक, जिसका भरण ज्यावक्रीय सिग्नल द्वारा किया गया है, के निर्गत् में बिना फिल्टर के शिखर वोल्टता का मान 10 V है। निर्गत् वोल्टता का DC अंश होगा
(a) [latex]\cfrac { 10 }{ \sqrt { 2 } } V [/latex]
(b) [latex]\cfrac { 10 }{ \pi } V[/latex]
(c) 10v
(d) [latex]\cfrac { 20 }{ \pi } V[/latex]
प्रश्न 2.
सभी खण्डों के उत्तर दीजिये। (1 x 6= 6)
(i) परावैद्युत सामर्थ्य से क्या अभिप्राय है?
(ii) अनुनाद परिपथ में L-C-R परिपथ के शक्ति गुणांक का मान बताइये।
(iii) 600 नैनोमीटर तरंगदैर्ध्य का प्रकाश विद्युत चुम्बकीय वर्णक्रम के किस भाग में होगा?
(iv) प्रकाश का वह अभिलक्षण बताइये, जो अपवर्तन की घटना में अपरिवर्तित रहता है।
(v) प्रकाश की तरंगदैर्घ्य बढ़ाने पर किसी माध्यम के अपवर्तनांक पर क्या प्रभाव पड़ता है?
(vi) आयाम मॉडुलन क्या है?
प्रश्न 3.
सभी खण्डों के उत्तर दीजिये। (2 x 4= 8)
(i) एक आवेश qको दो भागों में किस प्रकार विभाजित करें कि उन्हें एकदूसरे से कुछ दूरी पर रखने पर उनके बीच अधिकतम प्रतिकर्षण बल लगे?
(ii) प्रत्यावर्ती परिपथ के लिये औसत शक्ति का व्यंजक प्राप्त कीजिये।
(iii) हाइगेन्स के तरंग संचरण सम्बन्धी सिद्धान्त की व्याख्या कीजिये।
(iv) चित्र में दिये गये गेटो P तथा ५ के नाम बताइये तथा निर्गत् सिग्नल Y की सत्यता सारणी बनाइये।
प्रश्न 4.
सभी खण्डों के उत्तर दीजिये। (3 x 10 = 30)
(i) विभवमापी की सुग्राहिता किस प्रकार बढ़ाई जाती है? वोल्टमीटर की तुलना में इसे श्रेष्ठ क्यों समझा जाता है?
(ii) किसी धारामापी की कुण्डली का प्रतिरोध 15 ओम है। 4 मिली ऐम्पियर की वैद्यत धारा प्रवाहित होने पर यह पूर्ण स्केल विक्षेप दर्शाता है। आप इस धारामापी को से 6 ऐम्पियर परास वाले अमीटर में कैसे रूपान्तरित करेंगे?
(iii) एक धात्विक चालक का प्रतिरोध ताप बढ़ने पर बढ़ता है, जबकि अर्सचालक का प्रतिरोध ताप बढ़ने के साथ घटता है। कारण स्पष्ट कीजिये।
(iv) संलग्न चित्र में जुड़े तीन प्रतिरोध वाटों में प्रत्येक 22 है तथा प्रत्येक को अधिकतम 18 वाट तक विद्युत शक्ति दी जा सकती है (अन्यथा वह पिघल जायेगा)। पूर्ण परिपथ कितनी अधिकतम शक्ति ले सकता है?
(v) आयाम मॉडुलित e का मान ? = 150[1+ 0.5 cos 32501] cos 5 x 105 t से व्यक्त किया जाता है। गणना कीजिये।
(a) मॉडुलन सूचकांक
(b) मॉडुलन आवृत्ति
(c) वाहक आवृत्ति
(d) वाहक आयाम।
(vi) पतले लेन्स की फोकस दूरी के लिये न्यूटन के सूत्र का व्यंजक स्थापित कीजिये।
(vii) 25 वाट के एकवर्षीय प्रकाश स्रोत से उत्सर्जित तरंगदैर्ध्य 6000 A वाले फोटॉनों की प्रति सेकण्ड संख्या ज्ञात कीजिये। 5% प्रकाश वैद्युत प्रभाव दक्षता मानने पर, प्रकाश वैद्युत धारा क्या होगी?
(h = 6.6 x 10-34 जूल-सेकण्ड, c= 3.0 x 108 मी/से, e = 1.6 x 1019 कूलॉम)
(viii)
(a) हाइड्रोजन परमाणु में इलेक्ट्रॉन नाभिक के चारों ओर प्रति सेकण्ड 6 x 1015 चक्कर लगाता हैं। वृत्तीय पथ में धारा का मान क्या होगा?
(b) बोहर का परमाणु मॉडल रदरफोर्ड के परमाणु मॉडल से कैसे श्रेष्ठ है?
(ix)
(a) नाभिकीय श्रृंखला अभिक्रिया में क्रान्तिक द्रव्यमान से क्या ।अभिप्राय है?
(x) एक समतल वैद्युत चुम्बकीय तरंग में वैद्युत क्षेत्र 2.0×100 हर्ट्ज की आवृत्ति से ज्यावक्रीय रूप से दोलन करता है। इसका आयाम 48 वोल्ट/मी है। ज्ञात कीजिये।
(a) दोलित्र चुम्बकीय क्षेत्र का आयाम
(b) औसत वैद्युत ऊर्जा घनत्व
(c) औसत चुम्बकीय ऊर्जा घनत्व
प्रश्न 5.
सभी खण्डों के उत्तर दीजिये। (5 x 4= 20)
(i) गाँस की प्रमेय का उल्लेख कीजिए। एकसमान आवेशित गोलीय कोश के कारण वैद्युत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए, जबकि बिन्दु कोश के
(a) बाहर
(b) पृष्ठ पर
(c) अन्दर स्थित हो।
(ii) प्रत्यावर्ती धारा जनित्र की रचना एवं कार्यविधि समझाइए। दिष्ट धारा की तुलना में | प्रत्यावर्ती धारा के क्या लाभ हैं? जिनके कारण अब समान्यतः प्रत्यावर्ती धारा ही प्रयोग की जाती है।
(iii) प्रकाश के व्यतिकरण सम्बन्धी प्रयोग में दो स्लिटों के बीच अन्तराल 0.2 मिमी है। इनसे निर्गत् प्रकाश के व्यतिकरण से 1 मी दूरी पर स्थित पर्दे पर 3 मिमी चौड़ी फ्रिजें बनती हैं। गणना कीजिए
(a) स्लिटों पर आपतित प्रकाश की तरंगदैर्ध्य ।
(b) केन्द्रीय दीप्त फ्रिन्ज से तृतीय अदीप्त फ्रिज की दूरी
(iv)
(a) जेनर डायोड क्या होता है? इसके उपयोग समझाइये।
(b) दर्शाइये कि चित्र में दिया गया परिपथ OR गेट की भाँति व्यवहार करता है।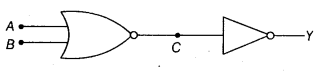
Answers
उत्तर 1(i).
(b) [latex]\cfrac { { r }_{ 2 }^{ 2 } }{ { r }_{ 1 }^{ 2 } } [/latex]
उत्तर 1(ii).
(b) बढ़ेगी।
यदि मुक्त इलेक्ट्रॉनों की धातु के धनायनों के साथ टक्करों की संख्या घटती है, तो इलेक्ट्रॉनों का अनुगमन वेग बढ़ जाता है, इसलिए धारा बढ़ जाएगी।
उत्तर (iii).
(b) लौहचुम्बकीय
डोमेन की रचना केवल लौहचुम्बकीय पदार्थों में होती है। डोमेन के कारण इनका चुम्बकत्व बहुत अधिक बढ़ जाता है।
उत्तर 5.
(b) उचित फोकस दूरी के उत्तल लेन्स के प्रयोग से
उत्तर 6.
(b) [latex]\cfrac { 10 }{ \pi } V[/latex]
उत्तर 2
(i) किसी परावैद्युत पदार्थ के लिये महत्तम अथवा अधिकतम वैद्युत क्षेत्र लिये बिना वैद्युत भंजन के सहन कर सकता है, परावैद्युत सामर्थ्य कहलाता है।

(vi) आयाम मॉडुलन वह क्रिया है, जिसमें उच्च आवृत्ति की वाहक तरंगों के आयाम मॉडुलक तरंग के तात्कालिक मान के अनुसार बढ़ता है।
उत्तर 3.
(ii) जब किसी वैद्युत परिपथ में प्रतिरोध (R) तथा प्रेरकत्व (L) दोनों हो, तो धारा । वोल्टेज V से φ कलान्तर पश्चगामी होती है, इस प्रकार के परिपथ में वोल्टेज एवं धारा के मान निम्न समीकरण से व्यक्त किए जाते हैं।
(iii) हाइगेन्स के तरंग संचरण सम्बन्धी सिद्धान्त के अनुसार,
(a) जब किसी माध्यम में स्थित तरंग स्रोत से तरंगें निकलती हैं, तो स्रोत के चारों ओर स्थित माध्यम के कण कम्पन करने लगते हैं। माध्यम में वह पृष्ठ जिसमें स्थित सभी कण कम्पन की समान कला में हों, तरंगाग्र कहलाता है।
(b) तरंगाग्र पर स्थित प्रत्येक कण एक नये तरंग स्रोत का कार्य करता है,जिससे नई तरंगें सभी दिशाओं में निकलती हैं। इन तरंगों को द्वितीयक तरंगिकाएँ कहते हैं।
(c) यदि किसी क्षण आगे बढ़ती हुई इन द्वितीयक तरंगिकाओं का आवरण (Envelope) उन्हें स्पर्श करते हुए पृष्ठ खींचे, तो यह आवरण उस क्षण तरंगाग्र की नई स्थिति प्रदर्शित करेगा।
(iv) P.NAND गेट तथा Q-OR गेट है।
उत्तर 4.
(i) विभवमापी की सुग्राहिता इसके तार की विभव प्रवणता के व्युत्क्रमानुपाती होती है। तार की विभव प्रवणता K =V/L जहाँ L तार की लम्बाई है। अतः स्पष्ट है कि L का मान जितना अधिक होगा अर्थात् विभवमापी के तार की लम्बाई जितनी अधिक होगी, उसकी विभव प्रवणता उतनी ही कम होगी, जिससे उसकी सुग्राहिता उतनी ही अधिक होगी। इस प्रकार विभवमापी के तार की लम्बाई बढ़ाने पर सुग्राहिता को बढ़ाया जा सकता है।
विभवमापी की वोल्टमीटर से श्रेष्ठता ।
(a) जब विभवमापी से सेल का वैद्युत वाहक बल नापते हैं, तो शुन्य विक्षेप की स्थिति में सेल के परिपथ में कोई धारा प्रवाहित नहीं। होती है अर्थात् सेल खुले परिपथ में होते हैं। अतः इस स्थिति में सेल के वैद्युत वाहक बल का वास्तविक मान प्राप्त होता है। इस प्रकार विभवमापी अनन्त प्रतिरोध के वोल्टमीटर के समतुल्य होता है।
(b) वोल्टमीटर द्वारा सेल का वैद्युत वाहक बल नापते समय विक्षेप पढ़ना होता है। विक्षेप के पढ़ने में त्रुटि हो सकती है, जबकि विभवमापी में । शुन्य विक्षेप की स्थिति पढ़नी होती है तथा तार की लम्बाई अधिक होती है। अतः इसमें प्रतिशत त्रुटि बहुत कम होती है।
(ii) यदि शन्ट का प्रतिरोध S तथा धारामापी का प्रतिरोध G हो, तो धारामापी में पूर्ण स्केल विक्षेप के लिए आवश्यक धारा ।
(iv)
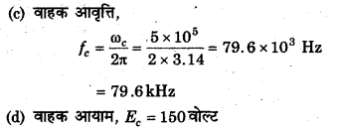
(vi) न्यूटन का सूत्र माना कि परिमित आकार की कोई वस्तु 00′ एक पतले उत्तल लेन्स की मुख्य अक्ष के प्रथम फोकस F’ के बायीं ओर अक्ष के लम्बवत् रखी है। 2′ से मुख्य अक्ष के समान्तर चलने वाली प्रकाश किरण लेन्स से अपवर्तन के बाद द्वितीय फोकस से जाएगी तथा प्रथम फोकस F” से जाने वाली किरण लेन्स से अपवर्तन के बाद मुख्य अक्ष के समान्तर हो जाती है। इस प्रकार 00′ का प्रतिबिम्ब II’ बनता है।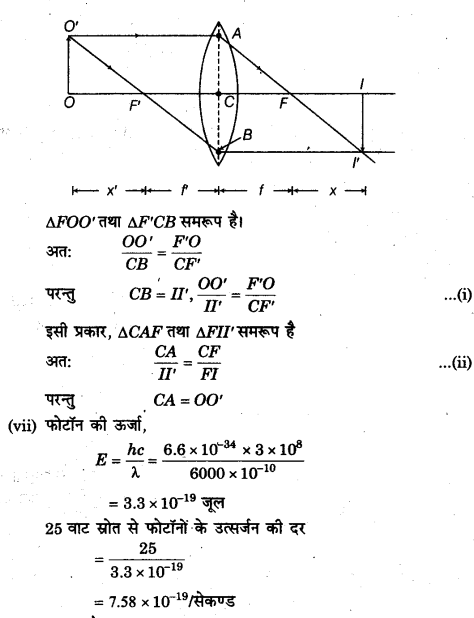

(b) रदरफोर्ड के परमाणु मॉडल के अनुसार, इलेक्ट्रॉन नाभिक के चारों ओर किन्हीं भी कक्षाओं में घूम सकते हैं जबकि बोहर मॉडल के अनुसार, इलेक्ट्रॉन केवल कुछ निश्चित त्रिज्याओं वाली कक्षाओं में ही घूम सकते हैं। रदरफोर्ड मॉडल के अनुसार, इलेक्ट्रॉन सभी आवृत्तियों की तरंगें उत्सर्जित करते हैं अर्थात् स्पेक्ट्रम सतत् होता है। बोहर मॉडल के अनुसार, इलेक्ट्रॉन केवल कुछ निश्चित आवृत्तियों की ही तरंगें उत्सर्जित करते है, जिनके कारण रैखिक स्पेक्ट्रम प्राप्त होता है।
(ix)
(a) किसी विखण्डनीय पदार्थ में श्रृंखला अभिक्रिया बनाये रखने के लिए, पदार्थ का द्रव्यमान एक विशेष मान से अधिक होना चाहिए अन्यथा विखण्डन से उत्पन्न अधिकांश न्यूट्रॉन आगे विखण्डन करने से पहले ही पदार्थ से बाहर निकल जायेंगे तथा अभिक्रिया बन्द हो जायेगी। अतः वह न्यूनतम द्रव्यमान जिससे कम पर श्रृंखला अभिक्रिया सम्भव नहीं है, क्रान्तिक द्रव्यमान कहलाता है।
उत्तर 5
(i) गॉस प्रमेय किसी बन्द पृष्ठ से गुजरने वाले वैद्युत फ्लक्स φEहै, उस पृष्ठ । द्वारा परिबद्ध कुल आवेश q का 1/ε0 गुना होता है।अर्थात् φE= q / ε0
माना R त्रिज्या के गोलीय कोश की सतह पर q आवेश समान रूप से वितरित है। इस गोले के केन्द्र 0 से दूरी पर बिन्दु P पर वैद्युत क्षेत्र का । मान ज्ञात करना है।
(a) जब बिन्दु गोलीय कोश से बाहर स्थित हो (r >R) अब, चित्र के अनुसार O को केन्द्र मानकर त्रिज्या r के एक गॉसीय पृष्ठ की कल्पना करते हैं। इस गोलाकार। पृष्ठ को गाँसियन पृष्ठ भी कहते हैं। समान दूरी पर होने के कारण, इस 0 पृष्ठ के प्रत्येक बिन्दु पर वैद्युत क्षेत्र E का परिमाण तो समान होता है। परन्तु उसकी दिशा अलग-अलग एवं उस बिन्दु पर त्रिज्यीय होती हैं। बिन्दु P पर गॉसीय पृष्ठ की सतह पर एक अल्पांश क्षेत्रफल dA लेते हैं, जिसके सदिश क्षेत्रफल की दिशा भी त्रिज्य होती है।

समी (iii) से स्पष्ट होता है कि बाह्य बिन्दु के लिए गोलीय कोश पर वितरित आवेश इस प्रकारे व्यवहार करता है जैसे कि सम्पूर्ण आवेश गोलीय कोश के केन्द्र पर स्थित हो।
(b) जब बिन्दु गोलीय कोश की सतह पर हो (r = R) जब बिन्दु गोलीय कोश की सतह पर होता है, तब उसके लिए केन्द्र से दूरी r = R होती है। अतः समी (ii) में r का मान । रखने पर
अतः स्पष्ट है कि आवेशित गोलीय कोश के कारण वैद्युत क्षेत्रका मान उसकी सतह पर अधिकतम होता है।
(c) जब बिन्दु गोलीय कोश के अन्दर स्थित हो (r<R) माना गोलीय कोश के अन्दर उसके केन्द्र 0 से r दूरी पर । एक बिन्दु P है, जिस पर । वैद्युत क्षेत्र E का मान ज्ञात करना है। चित्र के अनुसार, 0 को केन्द्र मानकर । त्रिज्या के एक गॉ सीय पृष्ठ की कल्पना करते हैं। चूँकि इस पृष्ठ के। अन्दर आवेश का मान शून्य। होता है, अत: इस पृष्ठ के लिए गॉस के नियम से,

अतः आवेशित गोलीय कोश के अन्दर वैद्युत क्षेत्र का मान शून्य होता है।
(ii) प्रत्यावर्ती धारा जनित्र अथवा डायनेमो एक ऐसी वैद्युत चुम्बकीय मशीन है, जिसके द्वारा यान्त्रिक ऊर्जा को वैद्युत ऊर्जा में बदला जाता है। प्रत्यावर्ती धारा को उत्पन्न करने के लिए प्रत्यावर्ती धारा डायनेमो तथा दिष्ट धारा को उत्पन्न करने के लिए दिष्ट्र धारा डायनेमो का उपयोग होता है। सिद्धान्त जब किसी बन्द कुण्डली को चुम्बकीय क्षेत्र में तेजी से घूर्णन कराया जाता है, तो उसमें से गुजरने वाली फ्लक्स रेखाओं की संख्या ‘ में लगातार परिवर्तन होता रहता है, जिसके कारण कुण्डली में वैद्युत धारा उत्पन्न हो जाती है। कुण्डली को घुमाने में जो कार्य करना पड़ता है अर्थात् जो यान्त्रिक ऊर्जा व्यय होती है। वही कुण्डली में वैद्युत ऊर्जा के रूप में प्राप्त होती है। रचना प्रत्यावर्ती धारा जनित्र के मुख्यतः तीन भाग होते हैं।
(a) क्षेत्र चुम्बक यह एक शक्तिशाली चुम्बक N-S होता है। इसके द्वारा । उत्पन्न चुम्बकीय क्षेत्र की बल रेखाएँ चुम्बक के ध्रुव N से S की ओर होती है। |
(b) आर्मेचर चुम्बक के ध्रुवों के बीच में पृथक्कृत ताँबे के तारों की एक कुण्डली ABCD होती है, जिसे आमेचर कुण्डली कहते हैं। कुण्डली कई फेरों की होती है तथा ध्रुवों के बीच क्षैतिज अक्ष पर पानी के टरबाईन से घुमाई जाती है।
(c) सप-वलय तथा ब्रश कुण्डली के सिरों को सम्बन्ध अलग-अलग दो ताँबे के छल्लों से होता है, जो आपस में एक-दूसरे को स्पर्श नहीं करते। हैं और कुण्डली के साथ उसकी अक्ष पर घूमते हैं, इन्हें सर्दी-वलय । कहते हैं। इन छल्लों को दो कार्बन के ब्रुश X तथा Y स्पर्श करते रहते । हैं। ये ब्रुश स्थिर रहते हैं तथा इन छल्लों के नीचे फिसलते हुए घूमते हैं। इन ब्रुशों का सम्बन्ध उस बाह्य परिपथ से कर देते हैं, जिसमें वैद्युत धारा भेजनी होती है।
कार्यविधि जब आमेचर कुण्डली ABCD घूमती है, तो कुण्डली में से होकर जाने वाली फ्लक्स रेखाओं की संख्या में परिवर्तन होता है। अत: कुण्डली में धारा प्रेरित हो जाती है। माना कुण्डली दक्षिणावर्त दिशा में घूम रही है तथा | किसी क्षण क्षैतिज अवस्था में है। इस क्षण कुण्डली की भुजा AB ऊपर उठ रही है तथा भुजा CD नीचे जा रही है। फ्लेमिंग के दाएँ हाथ के नियम के अनुसार, इन भुजाओं में प्रेरित धारा की दिशा वही है जो चित्र में प्रदर्शित है।
अतः धारा ब्रश x से बाहर जा रही है अर्थात् यह धन ध्रुव है तथा बुश Y पर वापस आ रही है अर्थात् यह ब्रुश ऋण ध्रुव है। जैसे ही कुण्डली अपनी ऊध्र्वाधर स्थिति से गुजरेगी भुजा AB की ओर आने लगेगी तथा CD ऊपर की ओर जाने लगेगी। अतः अब, धारा ब्रुश Y से बाहर जायेगी तथा बुश X पर वापस आयेगी। इस प्रकार आधे चक्कर के बाद बाह्य परिपथ में धारा की दिशा बदल जायेगी। अतः परिपथ में प्रत्यावर्ती धारा उत्पन्न होगी। प्रत्यावर्ती धारा की दिष्ट धारा की तुलना में उपयोगिता वर्तमान में घरेलू व औद्योगिक कार्यों में प्रत्यावर्ती धारा का ही उपयोग होता है, क्योकि दिष्ट धारा की तुलना में इसके निम्न लाभ हैं। |
(a) प्रत्यावर्ती धारा के पावर प्लांट से किसी स्थान पर ट्रान्सफॉर्मर की। सहायता से उच्च वोल्टेज पर भेजा जा सकता है तथा वहाँ इसे पुनः निम्न वोल्टेज पर लाया जा सकता है। इस प्रकार भेजने में लागत भी कम आती है तथा ऊर्जा ह्रास भी बहुत घट जाता है। ट्रान्सफॉर्मर का उपयोग दिष्ट धारा के लिए नहीं किया जा सकता। अतः दिष्ट धारा को एक स्थान से दूसरे स्थान पर भेजने में ऊर्जा हास भी । होता है तथा कीमत भी अधिक आती है।
(b) प्रत्यावर्ती धारा को चोक कुण्डली द्वारा बहुत कम ऊर्जा हास परनियन्त्रित किया जा सकता है, जबकि दिष्ट धारा ओमीय प्रतिरोध द्वारा ही नियन्त्रित की जा सकती है, जिसमें अत्यधिक ऊर्जा ह्रास होता है।
(c) प्रत्यावर्ती धारा वाले यन्त्र, जैसे-वैद्युत मोटर दिष्ट धारा वाले यन्त्रों की तुलना में सुदृढ़ व सुविधाजनक होते हैं।
(d) जहाँ दिष्ट धारा की आवश्यकता होती है, वहाँ दिष्टकारी द्वारा प्रत्यावर्ती धारा को सुगमता से दिष्ट धारा में बदल दिया जाता है।

जेनर डायोड के श्रेणीक्रम में एक प्रतिरोध है, को इस प्रकार संयोजित करते हैं कि जेनर डायोड उत्क्रम अभिनत हो जाए, क्योंकि भंजन क्षेत्र में जेनर वोल्टेज नियत बनी रहती है। अतः निवेशी वोल्टता में कमी । अथवा वृद्धि होने पर जेनर वोल्टता में बिना कोई परिवर्तन हुए प्रतिरोध R, के सिरों पर संगत परिवर्तन हो जाता है। इस प्रकार जेनर डायोड । एक वोल्टेज नियन्त्रक की तरह कार्य करता है। निर्गत् वोल्टता को । नियन्त्रित रखने के लिए तथा निवेशी वोल्टता को नियन्त्रित रखने के लिए तथा निवेशी वोल्टता को दी गई परास के लिए प्रतिरोध R, का मान इस प्रकार निर्धारित करते हैं कि जेनर डायोड भंजक क्षेत्र में प्रचलित हो तथा • जेनर डायोड में बहने वाली धारा का मान एक निश्चित मान से अधिक न हो, अन्यथा डायोड जल जाएगा।
(b) परिपथ में पहला गेट NOR गेट है। इसके निर्गत् को NOT गेट की निवेशी बनाया गया है, जिसका निर्गत Y है।
We hope the UP Board Class 12 Physics Model Papers Paper 1 help you. If you have any query regarding UP Board Class 12 Physics Model Papers Paper 1, drop a comment below and we will get back to you at the earliest.
जी हाँ आप अगर अपनी क्लास में अच्छे अंक प्राप्त करना चाहते है तो हमे अच्छे से follow करे और पाए हर एक पेपर में वो प्रश्न जो आपको मिलेंगे आपके एग्जाम में








